Richard Feynman, einer der bekanntesten Physiker des 20. Jahrhunderts, war überzeugt, dass niemand die Quantentheorie versteht. Über reguläre Ausdrücke, auch reguläre Expressionen genannt, könnte ähnliches behauptet werden. Vielleicht liegt es daran, dass diese Ausdrücke auf den ersten Blick einschüchternd aussehen können:
#?([\da-fA-F]{2})([\da-fA-F]{2})([\da-fA-F]{2})
Allerdings sind reguläre Ausdrücke nicht ganz so kontraintuitiv wie besagte Theorie und sind in der Entwicklung sowie im IT-Alltag ein Werkzeug, welches in vielen Fällen hilfreich zur Seite stehen kann, aber auch Grenzen hat.
Definition
Aus Sicht der theoretischen Informatik ist ein regulärer Ausdruck eine Methode, um Mengen von Zeichenketten mit gemeinsamen Mustern zu beschreiben. Reguläre Ausdrücke werden durch die Verwendung von verschiedenen Operatoren und Konventionen definiert, die es ermöglichen, komplexe Suchmuster zu erstellen.
Die Theorie der regulären Ausdrücke basiert auf den Konzepten der endlichen Automaten und der regulären Sprachen. Vereinfacht gesehen, kann die Funktionalität eines regulären Ausdrucks als Musterabgleich gesehen werden. Oft werden diese Ausdrücke als Regex oder Rexexp abgekürzt.
Ein einfacher regulärer Ausdruck könnte wie folgt aussehen:
[abc]
Dieser Ausdruck würde in einem Text die Zeichen a, b, und c finden. Über einen solchen regulären Ausdruck können Zeichenfolgen in Texten identifiziert, extrahiert und verarbeitet werden.
Geschichte
Die Geschichte regulärer Ausdrücke geht zurück auf das Jahr 1951, in welchem der Mathematiker Stephen Cole Kleene den Begriff prägte.
Praktische Anwendung fanden solche Ausdrücke in den 1960er-Jahren, als Ken Thompson, diese im Editor QED implementierte, als er diesen für das Compatible Time-Sharing System (CTSS) neuschrieb.
Über die Jahre wurde die Funktionalität regulärer Ausdrücke in weitere Werkzeuge wie grep und sed integriert. Im Rahmen der Unix-Philosophie, in welcher ein Werkzeug eine Aufgabe gut beherrschen soll, boten sich hiermit noch mächtigere Werkzeuge für die Textverarbeitung. Die Ausdrücke fanden nicht nur in der Textverarbeitung, sondern auch in der lexikalischen Analyse im Compiler-Design Anwendung.
Neben der Integration in solche Werkzeuge wurde vor allem beginnend mit den 1980er-Jahren die Integration regulärer Ausdrücke in Programmiersprachen wie Perl vorangetrieben. Einhergehend mit dieser Entwicklung wurde die Ausdrücke mächtiger und mehr Anwendungsfälle konnten mit diesen bearbeitet werden. Larry Wall, der Schöpfer von Perl, erweiterte die Fähigkeiten regulärer Ausdrücke erheblich und machte sie zu einem zentralen Bestandteil seiner Sprache.
In den 1990er-Jahren kam es zu einer Standardisierung von Syntax und Verhalten regulärer Ausdrücke, was die Entwicklung der Bibliothek der Perl-kompatiblen regulären Ausdrücke (PCRE) vorantrieb. Diese Bibliothek wurde in vielen Anwendungen verwendet und ist bis heute eine der am weitesten verbreiteten Implementierungen von regulären Ausdrücken.
Grundlagen
Doch wie genau werden reguläre Ausdrücke erstellt? Solche Ausdrücke können aus vielen unterschiedlichen Elementen bestehen, wie Literalen, Zeichenklassen, Quantifizierer und Gruppen.
So wäre ein regulärer Ausdruck bestehend aus einem einzigen Literal gültig:
a
Dieser Ausdruck würde hierbei auf die Vorkommen von a in einem Text matchen.
In regulären Ausdrücken können Oder-Verknüpfungen gebildet werden. So würde der Ausdruck:
a|b
entweder auf das Zeichen a oder auf das Zeichen b in einem Text matchen.
In den meisten Fällen wird allerdings nicht nach einem einzelnen Literal gematcht, sondern mit Zeichenklassen, Quantifizierern und Gruppen gearbeitet. Im Grundsatz würde allerdings nichts dagegen sprechen, einen regulären Ausdruck komplett, als Literal zu definieren:
Supercalifragilisticexpialigetisch
Diese Definition würde dazu führen, dass jedes Auftreten des Wortes Supercalifragilisticexpialigetisch gematcht werden würde. Allerdings wäre der reguläre Ausdruck in diesem Fall nicht mehr als eine einfache Suche.
Da es in regulären Ausdrücken eine Reihe von Zeichen mit spezieller Bedeutung gibt, müssen diese in bestimmten Fällen maskiert werden. Dies geschieht mit einem Backslash und dem sich anschließenden Zeichen:
\.
In diesem Beispiel würde der Punkt als normaler Punkt behandelt werden und nicht als Zeichen mit spezieller Bedeutung betrachtet werden.
Zeichenklassen
Zeichenklassen in regulären Ausdrücken erlauben es, eine Menge von Zeichen zu definieren, von denen jedes ein potenzielles Match für ein Zeichen aus dem Eingabetext darstellen kann. So würde der reguläre Ausdruck:
[abcdefghijklmnopqrstuvwxyz]
auf alle Zeichen zwischen a und z matchen. Die Zeichen werden hierbei in eckige Klammern eingefasst. Obiger Ausdruck kann allerdings sinnvoller gestaltet werden:
[a-z]
Der Bindestrich führt dazu, dass der Ausdruck als a bis z gelesen werden kann und damit einen Bereich definiert. Auch können mehrere Zeichenklassen in einem Block definiert werden:
[a-zA-Z]
Diese Zeichenklassen würde bei Buchstaben in Klein- und Großschreibung anschlagen. Bei dieser Notation ist darauf zu achten, dass die Definitionen ohne Leerzeichen aneinander gehangen werden.
Um auch deutsche Umlaute und das Eszett zu berücksichtigen, müssen diese Zeichen explizit zur Zeichenklasse hinzugefügt werden:
[a-zA-ZäöüÄÖÜß]
Standard-Zeichenklassen
Neben den selbstdefinierten Zeichenklassen existieren eine Reihe von vordefinierten Zeichenklassen, welche ebenfalls genutzt werden können.
So existiert die Zeichenklasse \d, welche allen Dezimalziffern entspricht, also 0 bis 9; dies entspricht der selbstdefinierten Zeichenklasse:
[0-9]
Die Zeichenklasse \D definiert das Gegenteil der vorherigen Klasse und matcht auf alle Nichtziffern und entspricht damit folgender Zeichenklasse:
[^0-9]
Während der Zirkumflex innerhalb einer Zeichenklasse normal genutzt werden kann, negiert er, am Anfang der Zeichenklasse stehend, diese. Eine Erweiterung dieser Standardklassen sind die Klassen \w und \W, welche für alle Wortzeichen stehen und folgenden selbstdefinierten Zeichenklassen entsprechen würden:
[a-zA-Z0-9_] [^a-zA-Z0-9_]
Daneben existieren, abhängig von der Implementierung weitere vordefinierte Zeichenklassen, wie \s für Whitespace-Zeichen oder die Klasse \S für alle Nicht-Whitespace-Zeichen.
Metazeichen
Im Rahmen regulärer Ausdrücke sind einige Metazeichen definiert, welche unterschiedlichste Bedeutungen haben und nicht als die Zeichen selbst interpretiert werden. Sie werden verwendet, um Muster für die Textsuche und -manipulation zu definieren. Einige dieser Zeichen sollen nachfolgend vorgestellt werden.
Der Punkt ist als Metazeichen so definiert, dass er für jedes beliebige Zeichen, bis auf einen Zeilenumbruch steht. Damit würde der Ausdruck:
a.c
unter anderem auf folgende Zeichenketten matchen:
aac abc acc
Solange ein a gefolgt von einem beliebigen Zeichen, wiederum gefolgt von einem c im Text vorkommt, wird dieses gematcht.
Der Zirkumflex markiert den Anfang einer Zeile bzw. eines Textes. Damit würde der reguläre Ausdruck:
^Lorem Ipsum
in einem gegebenen Beispieltext:
Lorem Ipsum abcdefghijklmnopqrstuvwxyz ABCDEFGHIKLMNOPQRSTUWXYZ Lorem Ipsum
das Auftreten von Lorem Ipsum am Anfang des Textes matchen. Die gegenteilige Operation kann mit dem Metazeichen $ erreicht werden:
Lorem Ipsum$
In diesem Fall würde das Lorem Ipsum am Ende des Beispieltextes gefunden werden.
Es ist wichtig zu beachten, dass innerhalb einer benutzerdefinierten Zeichenklasse die meisten Metazeichen, wie der Punkt oder der Stern, ihre spezielle Bedeutung verlieren und als normale Zeichen behandelt werden. Ausnahmen sind der Zirkumflex, wenn er als erstes Zeichen in der Klasse verwendet wird, um die Klasse zu negieren, der Bindestrich, um einen Bereich anzugeben, und der Backslash, um Escape-Sequenzen zu ermöglichen.
Quantifizierer
Quantifizierer (engl. Quantifiers) in regulären Ausdrücken sind spezielle Metazeichen, die angeben, wie oft das vorangehende Element in einem Textmuster vorkommen muss, um eine Übereinstimmung zu erzielen. Sie sind entscheidend, um die Flexibilität der Mustererkennung zu erhöhen.
Gegeben sei folgende Telefonnummer:
0176/04069015
Für diese Nummer könnte ein regulärer Ausdruck erstellt werden:
[0-9][0-9][0-9][0-9]/[0-9][0-9][0-9][0-9][0-9][0-9][0-9][0-9]
In dem Beispiel wurde auf Standardzeichenklassen verzichtet. Stattdessen wurden eigene Zeichenklassen definiert. Durch diesen Ausdruck werden die ersten vier Ziffern, dann ein Slash und anschließend die folgenden Ziffern gematcht.
Allerdings ist dieser Ausdruck weder sonderlich elegant, noch deckt er das Problem vollständig ab. Immerhin können Telefonnummern unterschiedlich lang sein und auch der Slash könnte optional sein. Hier kommen Quantifizierer zum Einsatz, von denen es eine Vielzahl mit diversen Anwendungsoptionen gibt.
Der Stern-Quantifizierer definiert, dass das vorangehende Element null- oder mehrmals vorkommt. So würde der Ausdruck:
a*b
unter anderem auf folgende Zeichenketten matchen:
ab aab aaab b
Die Anzahl der a’s vor dem Zeichen b sind hierbei unerheblich.
Das Plus-Quantifizierer definiert, dass das vorangehende Element mindestens einmal vorkommen muss. Damit würde der Ausdruck:
a+b
unter anderem auf folgende Zeichenketten matchen:
ab aab aaab
Ein Match auf eine Zeichenkette nur bestehend aus einem b wäre bei diesem Quantifizierer ausgeschlossen.
Zu dieser Gruppe von Quantifizierern gehört auch das Fragezeichen. Bei diesem kann das vorangehende Element null- oder einmal vorkommen. Damit würde der Ausdruck:
a?b
unter anderem auf folgende Zeichenketten matchen:
ab b
Ein Match auf eine Zeichenkette wie aab wäre bei dieser Variante ausgeschlossen.
Daneben existieren eine Reihe von komplexeren Quantifizierer wie den geschweiften Klammern, mit denen eine bestimmte Anzahl von Wiederholungen definiert werden kann. Der Ausdruck:
a{3}b
wurde spezifizieren, dass drei a’s hintereinander folgend von einem b gesucht werden. Damit würde dieser Ausdruck auf folgende Zeichenkette matchen:
aaab
Eine Erweiterung dieser Variante ist die Nutzung von Bereichen:
a{2,4}b
Hiermit würden alle Zeichenketten matchen bei denen zwischen zwei und vier a’s enthalten sind:
aab aaab aaaab
Eine weitere Abwandlung dieser Notationen ist es festzulegen, wie oft ein Element mindestens vorkommen muss:
a{2,}b
In diesem Fall müsste das Zeichen a mindestens zweimal vorkommen.
Mithilfe dieser Quantifizierer könnte der Ausdruck zum Match obiger Telefonnummer nun wesentlich vereinfacht werden:
[0-9]+/?[0-9]+
Damit ist der Ausdruck so definiert, dass eine beliebige Anzahl an Ziffern vorkommen können, gefolgt von einem optionalen Slash, wiederum gefolgt von einer beliebigen Anzahl an Ziffern.
Allerdings zeigt sich hier auch eine der Grenzen regulärer Ausdrücke: die Vielfalt möglicher Telefonnummernformate weltweit. Je nach Land und Region gelten unterschiedliche Regeln für den Aufbau einer Telefonnummer. Ein umfassender regulärer Ausdruck, der all diese Varianten abdeckt, könnte schnell sehr komplex werden und schwer zu warten sein.
In solchen Fällen kann es sinnvoll sein, zusätzliche Validierungslogik zu implementieren und nicht zu versuchen, die komplette Logik über einen regulären Ausdruck zu implementieren.
Gierige und faule Quantifizierer
Bei den beschriebenen Quantifizierern existieren gierige (engl. greedy) und faule (engl. lazy) Varianten. Gierige Quantifizierer versuchen, so viel wie möglich von der Zeichenkette zu erfassen, während sie den Regeln des regulären Ausdrucks folgen. Damit greifen sie den längstmöglichen Teil der Zeichenkette, der mit dem Muster übereinstimmt.
Faulen Quantifizierern hingegen geht es darum, so wenig wie möglich zu erfassen, während sie immer noch eine Übereinstimmung finden. Damit greifen sie den kürzestmöglichen Teil der Zeichenkette, der mit dem Muster übereinstimmt.
Quantifizierer sind im Normalfall gierig. Der Ausdruck:
a.*b
würde hiermit die Zeichenfolge:
ababab
als Ganzes matchen. Um diesen Ausdruck in der Lazy-Konfiguration zu betreiben, muss ein Fragezeichen nachgestellt werden:
a.*?b
In diesem Fall würden die ab-Blöcke jeweils einzeln gematcht werden.
Neben diesen beiden Varianten existieren noch possessive Quantifizierer. Solche Quantifizierer verhalten sich wie gierige Quantifizierer, aber sie geben einmal erfasste Zeichen nicht mehr frei.
Das kann das Matching verhindern, wenn der Rest des Musters nicht mehr passt. Possessive Quantifizierer können in bestimmten Situationen die Effizienz der Auswertung verbessern, da sie das aufwendige Backtracking unterbinden, können aber auch zu nicht intuitiven Ergebnissen führen, wenn sie nicht mit Bedacht eingesetzt werden.
Gruppierungen
Eine weitere Möglichkeit bei der Entwicklung regulärer Ausdrücke sind Gruppierungen. So würde der Ausdruck:
abc
nur auf die Zeichenkette abc matchen. Sollen hier jetzt auch Zeichenketten wie abcabc gematcht werden, können Klammern zur Gruppierung im Zusammenhang mit einem Quantifizierer genutzt werden:
(abc)+
Damit würden unter anderem folgende Zeichenketten auf den Ausdruck passen:
abc abcabc abcabcabc
Eine weitere Art von Gruppierung ist die Bildung von sogenannten Erfassungsgruppen. Mit diesen Gruppen, welche einen Teil des Ausdrucks ausmachen, kann später weitergearbeitet werden, z. B. in Form von Rückreferenzen:
(abc).*\1
In diesem Beispiel wird die Zeichenkette abc gesucht, welcher beliebige Zeichen folgen, bis schlussendlich wieder abc folgt. Dies wird über den Rückverweis auf die erste Erfassungsgruppe (\1) gelöst. Damit würde dieser Ausdruck unter anderem auf folgende Zeichenketten matchen:
abcabc abcloremabc abcipsumabc
Eine weitere Möglichkeit zur Nutzung von Gruppierung sind Oder-Verknüpfungen in einer Gruppe:
(a|b)c
Mit einer solchen Verknüpfung würden Zeichenketten wie ac und bc gematcht, allerdings nicht die Zeichenkette abc.
Daneben existieren Varianten wie verschachtelte Gruppen, benannte Gruppen oder nicht erfassende Gruppen, welche hier nicht weiter im Detail behandelt werden sollen.
Lookaround-Assertions
Eine weitere Möglichkeit zur Verfeinerung von regulären Ausdrücken sind Lookahead– und Lookbehind-Assertions. Im Deutschen könnte man diese Begrifflichkeiten mit vorwärts bzw. rückwärtsgerichtete Bedingungen grob übersetzen. Mit diesen kann die Umgebung eines Matches definiert werden.
So würde der Ausdruck:
Redaktion(?=skonferenz)
in einem Text auf das Wort Redaktion matchen, wenn es in der Zeichenkette Redaktionskonferenz enthalten wäre. Würde das Wort Redaktion alleine im Text stehen, so würde hier kein Match stattfinden. Bei dieser Variante handelt es sich um einen positiven Lookahead, da überprüft wird, ob das Muster nach dem Match vorkommt.
Das Gegenteil ist ein negativer Lookahead:
Redaktion(?!skonferenz)
Bei diesem würde auf das einzelne Wort Redaktion gematcht werden, auf das Wort Redaktion in der Zeichenkette Redaktionskonferenz allerdings nicht.
Neben den Lookahead-Assertions existieren analog dazu Lookbehind-Assertions welche prüfen, ob das Muster vor dem Match vorhanden ist:
(?<=Schluss)redaktion (?<!Schluss)redaktion
Ein komplexeres Beispiel für die Anwendung von Lookarounds könnte die Suche nach verschiedenen Schreibweisen des Wortes Hauptstraße sein. Ein regulärer Ausdruck, der Hauptstr., Hauptstraße und Hauptstrasse matcht, könnte wie folgt aussehen:
Hauptstr(aße|asse|\.)(?=\s|\b)
Hierbei sorgt die Lookahead-Assertion (?=\s|\b) dafür, dass das Match nur dann stattfindet, wenn das gesuchte Wort gefolgt von einem Whitespace (\s) oder einem Wortgrenzenzeichen (\b) steht. Diese Vorgehensweise verhindert, dass unerwünschte Matches wie Hauptstrasseneinmündung entstehen.
Flags
Neben den eigentlichen regulären Ausdrücken existieren eine Reihe von Optionen, welche das Verhalten der Engine zur Auswertung der regulären Ausdrücke anpassen.
So existiert mit der Global-Option (g) die Möglichkeit die Suche im gesamten Text durchzuführen und nicht nur bis zur ersten Übereinstimmung. Mit der Option i ignoriert die Engine die Groß- und Kleinschreibung im Rahmen der Mustererkennung.
Die Option Multiline (m) verändert das Verhalten für die Zeichen ^ und $, sodass sie nicht mehr nur den Start und das Ende des gesamten Textes markieren, sondern den Anfang und das Ende jeder einzelnen Zeile analysieren. Über die Singleline– bzw. Dotall-Direktive (s) kann der Punkt als Wildcard-Zeichen auch über die Grenzen der Zeilenumbrüche hinweg arbeiten.
Mit der Unicode-Option (u) kann bei einigen Engines die Auswertung von Unicode-Zeichen aktiviert werden.
Gesetzt werden können diese Flags als Teil des regulären Ausdrucks, so z. B. für das Global-Flag in Verbindung mit der Ignorierung der Groß- und Kleinschreibung:
(abc)/gi
Je nach verwendeter Engine werden diese Flags auch anders gesetzt, z. B. in Java beim Anlegen eines Pattern:
Pattern pattern = Pattern.compile(regex, Pattern.CASE_INSENSITIVE); Matcher matcher = pattern.matcher(text);
Daneben existieren in einigen Engines bestimmte Flags nicht, z. B. da Java bereits so konzipiert ist, dass die Engine alle Übereinstimmungen in einem gegebenen Text finden kann. Damit entspricht dieses Verhalten dem Global-Flag.
Unterschiede
Obwohl die grundlegenden Konzepte von regulären Ausdrücken über verschiedene Sprachen hinweg ähnlich sind, gibt es Unterschiede in der Syntax und Funktionalität, die Entwickler beachten müssen.
Einige Engines bieten erweiterte Funktionen wie Lookahead– und Lookbehind-Assertions, andere unterstützen benannte Gruppen. Die Unterstützung für Unicode ist ebenfalls ein Unterscheidungsmerkmal, da manche Engines in der Lage sind, mit einer Vielzahl von Zeichensätzen und Sprachen umzugehen, während andere auf ASCII beschränkt sind.
Trotz der Vielfalt unter den Engines haben sich viele Gemeinsamkeiten herausgebildet. Dazu gehören Metazeichen wie den Punkt für jedes Zeichen, den Stern für null oder mehr Wiederholungen, das Plus für eine oder mehr Wiederholungen und das Fragezeichen für null oder eine Wiederholung. Ebenso sind Zeichenklassen, Negationen, Anker für Anfang und Ende einer Zeichenkette, und einfache Quantifizierer weitgehend identisch.
Reguläre Ausdrücke in der Entwicklung
Bei der Anwendung regulärer Ausdrücke in der Entwicklung sind die jeweiligen Gegebenheiten der Programmiersprachen zu berücksichtigen. Ein Beispiel hierfür ist die Java-Methode zum Matchen in der Stringklasse:
String text = "3";
boolean matches = text.matches("[123]");
Hier wird die matches-Methode genutzt, um zu überprüfen, ob der gesamte String text dem regulären Ausdruck entspricht. Diese Herangehensweise ist für einmalige Überprüfungen einfach und direkt. Allerdings ist es ineffizient, wenn der gleiche Ausdruck in einer Schleife oder mehrfach im Code verwendet wird, da bei jedem Aufruf der Ausdruck neu kompiliert wird.
Alternativ kann diese Operation anders implementiert werden:
Pattern pattern = Pattern.compile("[123]");
boolean matches = pattern.matcher(text).matches();
Diese Variante ist effizienter, wenn der gleiche Ausdruck mehrfach genutzt werden soll. Hier wird das Pattern einmal kompiliert und kann anschließend mehrfach verwendet werden, ohne dass es jedes Mal neu kompiliert werden muss.
Reguläre Ausdrücke in Anwendungen
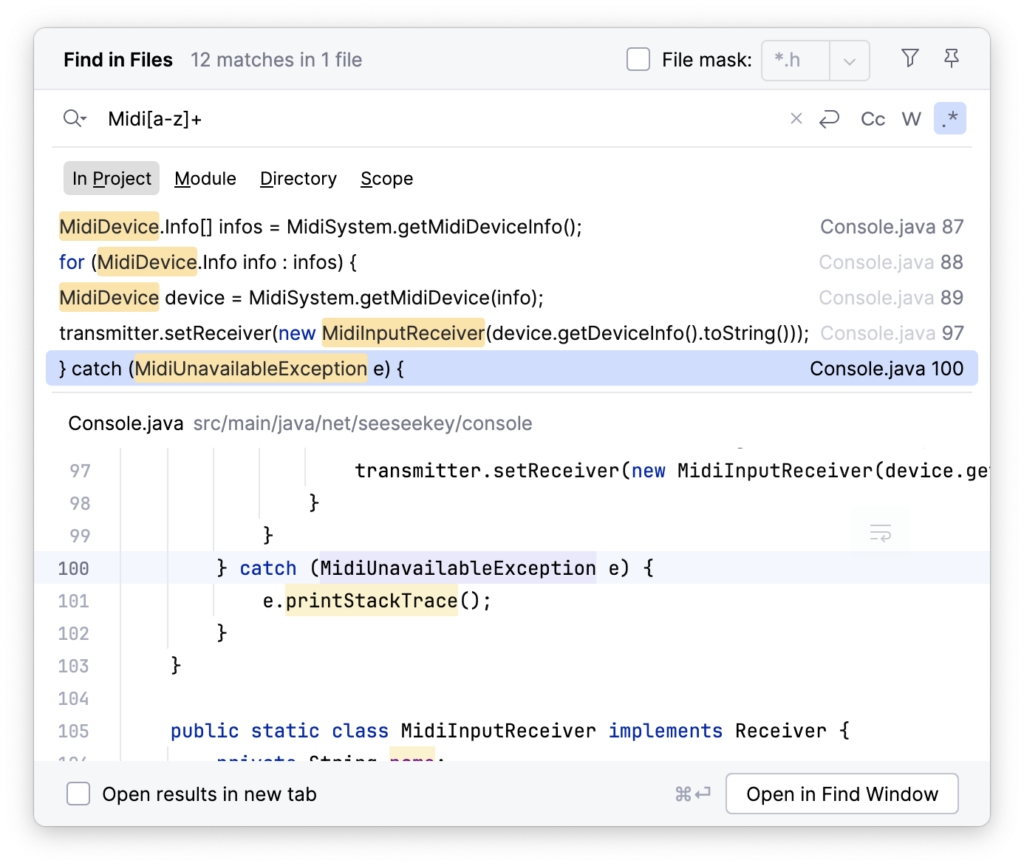
Neben der direkten Nutzung regulärer Ausdrücke in der Entwicklung, existieren unzählige Tools, wie Texteditoren oder Kommandozeilenwerkzeuge wie grep, welche ebenfalls Unterstützung für reguläre Ausdrücke liefern.
Für grep könnte dies wie folgt aussehen:
grep -E "G{1}N" gpl3.txt
Auch Texteditioren und IDEs enthalten Suchmethodiken, um über reguläre Ausdrücke zu finden.
Damit ist es möglich, Textstellen zu finden, die komplexeren Mustern entsprechen und mit einer einfachen Suche nicht ohne weiteres gefunden werden können.
Nutzung
Reguläre Ausdrücke sind ein mächtiges Werkzeug, wenn es darum geht, Benutzereingaben zu validieren. Sie werden häufig verwendet, um sicherzustellen, dass E-Mail-Adressen, Telefonnummern und andere Formen von Daten bestimmten Mustern entsprechen.
So könnte mit einem solchen Ausdruck z. B. die Validität einer E-Mail-Adresse überprüft werden:
[a-z0-9!#$%&'*+/=?^_`{|}~-]+(?:\.[a-z0-9!#$%&'*+/=?^_`{|}~-]+)*@(?:[a-z0-9](?:[a-z0-9-]*[a-z0-9])?\.)+[a-z0-9](?:[a-z0-9-]*[a-z0-9])?
Daneben können sie beim Parsen von Zeichenketten genutzt werden, z. B. um spezifische Informationen aus einem Text wie einer Logdatei herauszufiltern.
In der Compiler-Konstruktion werden reguläre Ausdrücke verwendet, um Tokens zu identifizieren, indem sie Muster definieren, die Schlüsselwörter, Operatoren oder andere syntaktische Elemente erkennen. Auch bei der Textbearbeitung, wie dem massenhaften Ersetzen, können reguläre Ausdrücke ihre Stärke ausspielen.
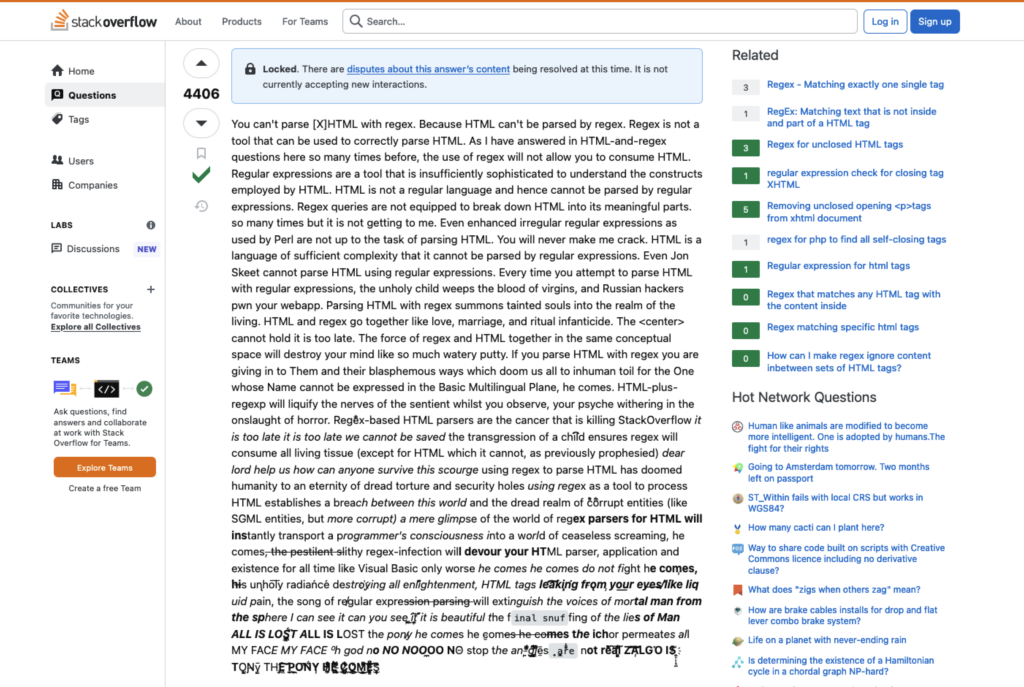
Trotzdem sollte nicht vergessen werden, dass sich reguläre Ausdrücke nicht für alle Zwecke eignen. So sollte z. B. davon abgesehen werden, nicht formale Sprachen mit regulären Ausdrücken zu parsen. Für das Parsen von HTML mittels regulärer Ausdrücke existiert dazu ein geradezu legendärer Post bei Stack Overflow, der sich dieses Problems annimmt.
Best Practices
Werden reguläre Ausdrücke genutzt, so sollten einige Best Practices berücksichtigt werden. Bei unsachgemäßer Verwendung kann ein regulärer Ausdruck schnell unübersichtlich und schwer wartbar werden kann.
So sollten genutzte reguläre Ausdrücke kommentiert werden und ihre Fachlichkeit darlegen, um das Verständnis zu erhöhen.
Anstelle von nummerierten Rückreferenzen lassen sich, wenn unterstützt, benannte Gruppen nutzen. Einige Engines erlauben auch die Verwendung von Leerzeichen und Zeilenumbrüchen in den Ausdrücken, was hilft, sie besser zu strukturieren. Zudem kann es vorteilhaft sein, lange und komplexe Muster in kleinere, wiederverwendbare Teile zu zerlegen, was die Wartung und das Verständnis des Ausdrucks erleichtert.
Es ist ratsam, in regulären Ausdrücken so spezifisch wie möglich zu sein. Anstatt generische Zeichen wie den Punkt, der jedes Zeichen repräsentieren kann, zu verwenden, sollten präzisere Zeichen oder Zeichenklassen gewählt werden. Dies hilft, unnötiges Backtracking zu vermeiden, das die Performance beeinträchtigen kann.
Obwohl Lookaround-Assertions in bestimmten Situationen sehr nützlich sein können, sollten sie mit Bedacht eingesetzt werden, da sie bei komplexen Mustern und großen Textmengen die Performance negativ beeinflussen können. Auch bei der Verwendung von Gruppierungen gilt gleiches, denn jede zusätzliche Gruppierung bedeutet mehr Aufwand bei der Verarbeitung des Ausdrucks.
Schließlich ist es unerlässlich, dass reguläre Ausdrücke gründlich getestet werden. Idealerweise sollte dies mit einer breiten Palette von Testfällen geschehen, um sicherzustellen, dass sie in jeder erwarteten Situation korrekt funktionieren.
Unter der Haube
In der alltäglichen Anwendung werden regulären Ausdrücke von einer Engine ausgeführt. Ein kurzer Blick in eine solche Engine, kann sich lohnen, da es hilft zu verstehen, wie reguläre Ausdrücke sinnvoll gestaltet werden können. Eine Engine, die diese Ausdrücke verarbeitet, kann entweder textorientiert oder regex-orientiert sein.
Eine textorientierte Engine, implementiert als deterministischer endlicher Automat (DFA), analysiert den Eingabetext sequenziell. Diese Methode ist schnell und effizient, da sie keine alternativen Pfade verfolgt und somit kein Backtracking benötigt. DFAs liefern stets die längste Übereinstimmung und sind aufgrund ihrer deterministischen Natur in der Performance vorhersehbar.
Im Gegensatz dazu steht die regex-orientierte Engine, die auf einem nichtdeterministischen endlichen Automaten (NFA) basiert. Eine solche Engine ist in der Lage, mehrere Pfade gleichzeitig zu verfolgen und bei Bedarf mittels Backtracking alternative Wege zu untersuchen. Dies ermöglicht eine flexible Mustererkennung, kann jedoch bei komplexen Ausdrücken zu einer erhöhten Rechenlast führen. NFAs priorisieren die am weitesten links stehende Übereinstimmung und können bei mehreren möglichen Matches zu einer kürzeren Übereinstimmung führen, selbst wenn weiter rechts im Text eine längere vorhanden wäre.
Moderne Regex-Engines sind meist regex-orientiert und nutzen einen Preprozessor, um den regulären Ausdruck vorzuverarbeiten, etwa um Makros in Zeichenklassen umzuwandeln. Anschließend wird der Ausdruck kompiliert, wobei er in eine effiziente Form überführt wird, die entweder als Reihe von Instruktionen oder als Zustandsautomat von der Engine verarbeitet werden kann.
Die Wahl der Engine hängt von den spezifischen Anforderungen der Aufgabe ab. Während DFAs für einfache, vorhersehbare Suchvorgänge geeignet sind, bieten NFAs die notwendige Flexibilität für komplexere Mustererkennungen.
Risiken und Nebenwirkungen
Neben der Möglichkeit reguläre Ausdrücke für Aufgaben zu nutzen, für die sie nicht geeignet sind, existieren auch andere Probleme, die mit diesen Ausdrücken zusammenhängen.
So gibt es den Regular expression Denial of Service-Angriff (ReDoS), welcher ausnutzt, dass viele Engines für reguläre Ausdrücke bei bestimmten Ausdrücken extrem langsam werden und viele Systemressourcen beanspruchen können.
Ein schönes Beispiel für eine solche Anfälligkeit, war der Ausfall von Stack Overflow im Jahre 2016. Dieser wurde durch einen Post mit zu vielen Leerzeichen verursacht, welcher dazu führte, dass die auf Backtracking basierte Engine über 199 Millionen Überprüfungen durchführen musste.
Allerdings gibt es Alternativen zu Backtracking nutzenden Engines, wie RE2 von Google. Diese Engine garantiert, basierend auf einem endlichen Automaten, eine lineare Ausführungszeit, bezogen auf die Eingabedaten und ist trotzdem mit den Features moderner Engines ausgestattet.
Werkzeuge
Für die Nutzung und Erstellung von regulären Ausdrücken existieren hilfreiche Werkzeugen. Zu diesen Werkzeugen gehören eine Reihe von Online-Testern. Dies sind interaktive Werkzeuge, die es dem Nutzer ermöglicht, regulären Ausdrücke in Echtzeit zu testen und zu debuggen. Diese Werkzeuge bieten oft farblich hervorgehobene Übereinstimmungen und Erklärungen für jedes Element des Ausdrucks.
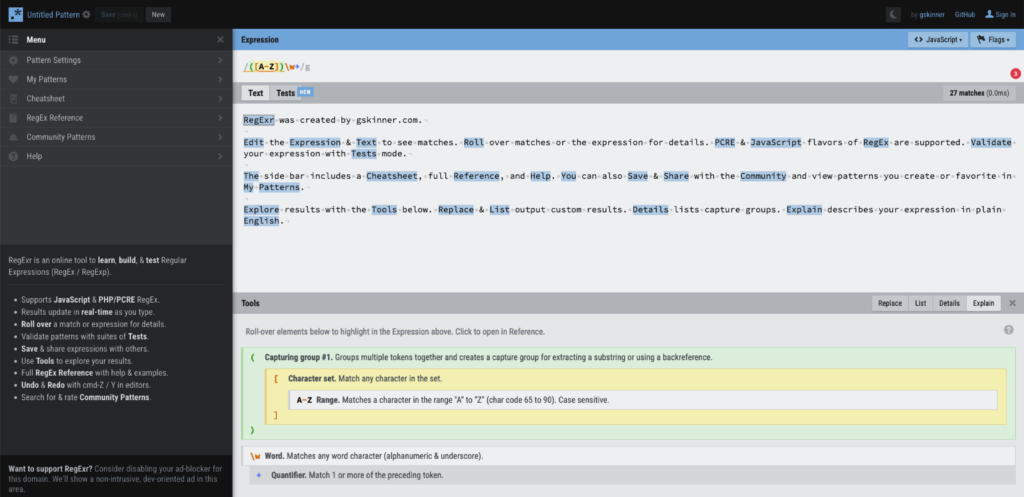
Einer dieser Tester ist RegExr, welcher unter regexr.com zu finden ist.
Neben der interaktiven Oberfläche bietet RegExr eine Referenz und eine große Anzahl von Community Patterns, die viele Probleme bereits abdecken und so die Entwicklung eines eigenen Ausdrucks beschleunigen können.
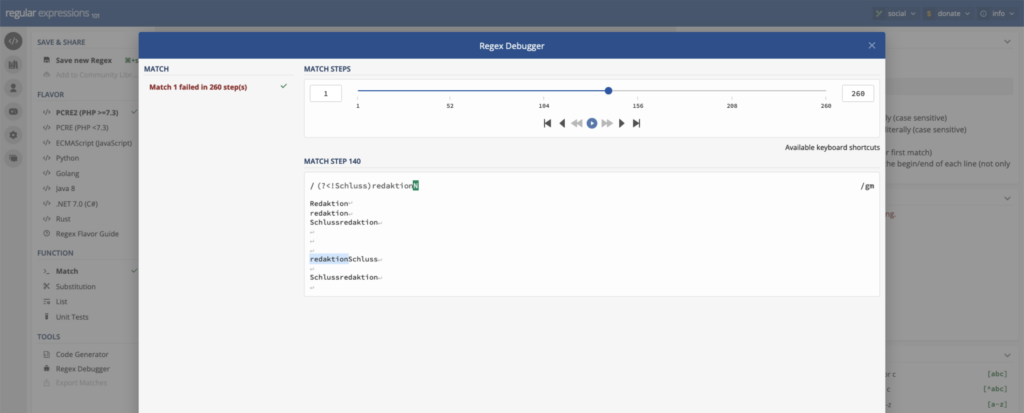
Ein weiterer Tester für reguläre Ausdrücke ist regular expressions 101, welcher unter regex101.com zu finden ist.
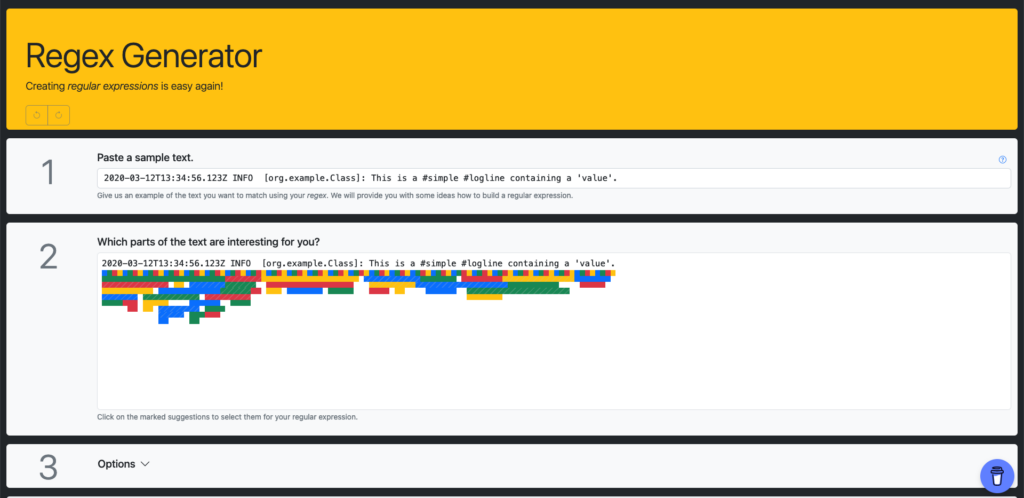
Eine Besonderheit dieses Dienstes ist der integrierte Debugger, mit welchem regulären Ausdrücke analysiert werden können. Einen umgekehrten Weg geht der Regex Generator von Olaf Neumann.
Mithilfe dieses Werkzeuges können reguläre Ausdrücke anhand eines Datenbeispieles erzeugt werden. Kommandozeilenwerkzeuge wie rgxg arbeiten nach ähnlichen Prinzipien und können auch offline genutzt werden.
Fazit
Insgesamt sind reguläre Ausdrücke ein mächtiges Werkzeug, um Textmuster zu durchsuchen und zu manipulieren. Sie ermöglichen eine effiziente Verarbeitung von Texten und sind daher ein wichtiges Werkzeug für Entwickler und Anwender. In der Praxis werden sie in verschiedenen Bereichen eingesetzt, um Texte zu durchsuchen, zu filtern und zu manipulieren.
Durch die Einhaltung von Best Practices und dem damit verbundenen Vermeiden häufiger Fehler können Entwickler sicherstellen, dass ihre regulären Ausdrücke sowohl leistungsfähig als auch wartbar sind.
Dieser Artikel erschien ursprünglich auf Golem.de und ist hier in einer alternativen Variante zu finden.